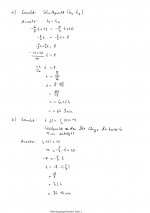Frage zur linearen Funktion

[Alteshaus21]

Moin
Da ich mitbekommen habe, das sich hier einige mit Mathekentnissen rumtreiben, dachte ich mir, stelle ich hier einfach mal meine Frage.
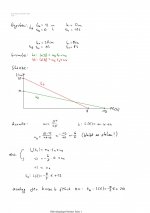
Wir haben eine Aufgabe bekommen. Es ist eine Tabelle in der P(x1/y1) und Q(x2/y2) gegeben sind. Wir müssen nun f(x), m= und n= angeben.
Die ersten Punkte die ich habe sind p(-8/2) und Q(2/2). Gerechnet habe ich dann m=(y2-x2) : (x2-x1).
Da kommt null raus. Kann das überhaupt sein?
Wie muss ich danach weiter vorgehen? Es heißt ja, y=mx + n. Muss ich dann m einsetzten also die Null, und für y y2 oder y1 einsetzen um damit b zu berechen?

Danke für Hilfe!

 

[Alteshaus21]

Yes

 

[Thomebau]

Eigentlich kann man die Gleichung direkt aufstellen ohne großartig was zu rechnen, aber wehe man hat unschönere Werte oder man hat nicht l[SUB]0[/SUB] gegeben, sondern z.B. die Länge bei 3h...

 

[Alteshaus21]

Hör mir auf
Jetzt grübel ich erstmal darüber, wies nun weiter geht. Die Graphen habe ich inzwischen gezeichnet.
Muss ich mit der Formel, y=mx+b noch was machen? Kann ich damit irgendwie die verschiedenen längen zur verschiedenen Zeitpunkten berechnen?

 

[Thomebau]

Kann ich damit irgendwie die verschiedenen längen zur verschiedenen Zeitpunkten berechnen?

Logo, dafür ist die Funktion ja da!

Jetzt überleg mal, die Aufgabenstellung für Teil a) lautet :"Die beiden Kerzen werden gleichzeitig angezündet. Wann sind sie gleich lang?"
Was ist gesucht?
Spoiler: >Gesucht ist also der Zeitpunkt, an dem die beiden Längen identisch sind.< (markieren zum lesen)

Den Rest solltest du wieder alleine hinbekommen.

 

[Alteshaus21]

Das was gesucht ist, also der Zeitpunkt ist mir klar. Mal sehen wie ich das hinbekomme.
Ist das nicht so mit Schnittpunkt der beiden Graphen? "Da war im Unterricht doch was"
Geht mit einem Gleichungssystem oder?

 

[Thomebau]

genau

 

[cuco]

Extra für dich: die übervollständige Lösung:
[Bild]
d.h.: Du hattest recht! Was auch ganz schnell klar wird wenn man sich die Funktion veranschaulicht: Zwei Punkte mit der selben Y-Koordinate spannen immer eine lineare Funktion auf welche konstant ist (m=0).

EDIT: Kleine Anmerkung am Rande: Wenn Delta-Y=0 wird handelt es sich um keine Funktion! Denn dann hätten beide Punkte die selbe Y-Koordinate und eine Funktion muss immer eindeutig sein.

Kleine Anmerkung: Beim Ausrechnen der Steigung aus dem Steigungsdreieck musst du DeltaY durch DeltaX teilen, nicht umgekehrt. Deine Rechnung "2-2" wäre dann auch DeltaY, nicht DeltaX - das wäre "2-(-8)=10", aber in der Rechnung egal, da DeltaY ja eh 0 ist. Ebenso muss DeltaX ungleich 0 sein, damit das ganze eindeutig wird.

 

[Thomebau]

äh jo, sehe ich auch grade ^^
Mist...

 

[dsred]

In welcher Klasse rechnet man das? (8./9.Klasse)?
Ich frage nur aus reiner Interesse, weil es bei mir schon eine gefühlte Ewigkeit her ist;-)

gruß dsred

 

[Alteshaus21]

In welcher Klasse rechnet man das? (8./9.Klasse)?
Ich frage nur aus reiner Interesse, weil es bei mir schon eine gefühlte Ewigkeit her ist;-)

gruß dsred

10 klasse Realschule hatten wir das schonmal. Jetzt 11. Klasse wirtschaftsgymnasium. In der 11 macht man ja sozusagen den Stoff der 10. nochmal also wenn man 3 Jahre Abitur hat, und nix verkürzt.

 

[Thomebau]

So, hab das oben mal korrigiert.
@Alteshaus: Was nu, wie weit biste?

 

[dsred]

na dann sind es bei mir ja erst 19 Jahre;-) Danke für die Info und viel Vergnügen.

Dass Schulmathe echt nützlich sein kann, hab ich erst kürzlich wieder erleben dürfen (Berechne die Geradengleichung, die den Massenschwerpunkt aus i Atomen (Mi) mit dem Massenschwerpunkt von j Atomen (Mj) verbindet). Daher immer schön am Ball bleiben...

Gruß dsred

 

[Thomebau]

Hmmm, da er mir nicht mehr als online angezeigt wird poste ich jetzt einfach mal meine Lösung, bevor ich das nachher vergesse.
Für Fehler übernehme ich aber keine Verantwortung

 

[Alteshaus21]

Thome danke! Ich mache morgen weiter. Danach schaue ich mir die Lösung genauer an

 

[Danton]

Also bei uns hamma das auch bei G8 in der 7 und 8 gemacht...*g*

 

[Thomebau]

wir eigentlich auch...

 

[Alteshaus21]

Also nochmal danke an Thome :thumbup: Habe das dann auch alles so herausbekommen!
und übrigens, wir haben das doch tagsächlich auch in der 8. Klasse gemacht