Für Mathe-Asse !! Jetzt: Irrationale Gleichung (s.u.)

[Pommbaer]

Ich habe hier ne Goniometrische Gleichung. Die Lösung hatte ich schnell, allerdings ist nur eine Lösung und ich würde gerne wissen nach welchem Schema ich auf die weiteren komme:

2 sin (x) * tan (x) = 6 cos (x) -> tan (x) auflösen in sin (x) / cos (x)

2 sin (x) * sin (x) / cos (x) = 6 cos (x) -> beide Seiten mit cos (x) multiplizieren

2 sin² (x) = 6 cos² (x) -> durch zwei Teilen

sin² (x) = 3 cos² (x) -> sin (x) umwandeln in Wurzel(1-cos² (x))

1 - cos² (x) = 3 cos² (x) -> cos² (x) addieren

1= 4 cos² (x)

x = arccos ( Wurzel ( 1/4 )) = 60

Soweit meine Lösung. Ich weiss, dass in diesem Fall auch alle 60 + k*Pi die richtige Lösung darstellen.
die Lösungsvorgabe sagt jedoch aus, dass auch alle 120 + k*Pi die richtige Lösung ergeben. k natürlich nur aus der Menge der reellen Zahlen.
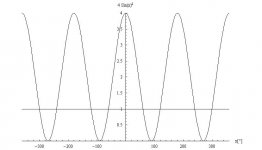
der Weg zu dieser Erkenntnis ist mir noch schleierhaft. Habe die Cosinuskurve aufgezeichnet aber kann keine "Regel" erkennen wie ich von meiner Lösung auf die zweite LÖsung komme.

ich denke hier wird der eine oder andere sein, der mir da weiterhelfen kann.

 

[PeterWa]

bis zur vorletzten Gleichung ist alles ok, dann würde ich 2 Gleichungen betrachten:
cos x = 1/2 und cos x =-1/2,
da beide die Gleichung 1= 4 cos² (x) erfüllen

 

[Schnitzel2k8]

Peter hat es schon richtig gesagt, wenn es um Wurzeln und Quadrate geht muß man sehr vorsichtig mit Vorzeiche sein. Du kannst aber deine zweite Lösung (120°+k*Pi) auch als -60°+n*Pi, mit n=k+1 interpretieren. Vielleicht siehst du es dann einfacher, da der Cosinus ja eine symmetrische Funktion ist.

 

[Pommbaer]

Danke

Nach euren Einwänden und einem genaueren Blick in die Formelsammlung sah ich doch tatsächlich,dass bei der Umwandlung von Sin(x) sowohl + als auch - Wurzel (1-cos²(x)) rauskommen kann.
Da steh dann also das Vorzeichen mit dem man auch auf 120 +k*Pi kommt.

Ich frage mich ob man nicht gleich einen Schritt weitergehen kann, und als Lösung allgemein 60*k angeben kann. Denn da Pi=180 auch ein vielfaches von 60 ist, würde jede Lösung 60*k mit k€R zum richtigen Ergebnis führen.

Danke nochmal !

 

[Schnitzel2k8]

Ich frage mich ob man nicht gleich einen Schritt weitergehen kann, und als Lösung allgemein 60*k angeben kann. Denn da Pi=180 auch ein vielfaches von 60 ist, würde jede Lösung 60*k mit k€R zum richtigen Ergebnis führen.

Kurz gesagt: Nein, z.B. 180° (k=3) ist keine Lsg!

Nachtrag: Hier mal ein Plot der Fkt 4 Cos(x)² und der Konstanten 1

Alle Schnittpunkte der beiden sind deine gesuchten Lösungen

Anhang anzeigen 34412

 

[Pommbaer]

Okay nehme ich so auf.

Ergibt sich sowas wie in diesem Fall denn immer aus der Gleichung oder gibt es auch eine Möglichkeit wenn man eine Lösung erhält mehrere Lösungen zu ermitteln OHNE das ganze zu Plotten ? Das ist in der Klausur nämlich nicht ohne Weiteres möglich und Zeit ist das Gold wert.
Also gibt es irgendeine Regel oder Formel nach der man aus dem 60° auch 120° erhält die aber allgemeine Gültigkeit hat bei goniometrischen Gleichungen ? Wie zB dass bei 60° auch -60° generell die Lösung sind ?

 

[Schnitzel2k8]

Deine Lösungszweige entstehen hier nur wegen der Wurzel. Du mußt ja in Wirklichkeit zwei Gleichungen lösen:

Cos(x)=1/2

Cos(x)= - 1/2

Aufgrund der Art der Gleichungen benötigst du in diesem Fall für jeden Zweig eine Lösung, die restlichen kannst du aufgrund der Periodizität des Cosinus ableiten.

 

[PeterWa]

jo, wie Schnitzel2k8 schon sagte, man verliert leicht eine Lösung, wenn man bei einer Gleichung auf beiden Seiten die Wurzel zieht und dabei nur das positive Vorzeichen betrachtet;

solange es um Schnitte einer trigonometrischen Funktion mit einer waagerechten Geraden handelt, ist das ganze noch recht übersichtlich; Empfehlung für die Klausurvorbereitung: einfach mal in einer halben Stunde die Schnittpunkte einer waagerechten Geraden mit sin x oder cos x oder tan x oder cot x oder sin² x oder cos² x auf kariertes Papier skizzieren; das muss man ja nicht plotten

wenn es sich nicht mehr um waagerechte Geraden handelt, wirds schon deutlich vertrackter: da kann es z.B. mit sin x einen Schnittpunkt geben oder je nach Steigung auch 3784 Schnittpunkte oder auch irgendeine andere Zahl; allerdings läßt sich so ein Problem in der Regel dann nur noch numerisch/näherungsweise und nicht mehr exakt lösen

 

[Pommbaer]

Dann hab ich auch schon wieder eine neue Frage.

ich komme nicht weiter bei einer irrationalen Gleichung:

2x^(2/3) - 5x^(1/3) = 3

Ich habe gerade keinen Schimmer wie ich das 1/3 aus dem exponenten kriegen soll.

 

[Schnitzel2k8]

x=27,

 

[Evilandi666]

Bei: 2x^(2/3) - 5x^(1/3) = 3 -> Lsg: 27 (Maple sagt das zumindest).

Von Hand geht das wohl so:

Beide Seiten hoch 3 nehmen. Dann steht links (..) ³ was gleich (..)² * (...) , also mit Binomischer Formel machbar, alternativ gibts auch eine "kubische" Binomische formel.

Nach ewig nervigem rumgerechnet sollte 27 rauskommen...

Achja und x^(2/3) = 3 Wurzel aus (x²)

 

[Schnitzel2k8]

Als kleiner Tip: Versuchs mal mit Substitution: y=x^(1/3)

 

[Evilandi666]

Schnitzel hat recht...

y= x^(1/3)

dann steht da: 2y² - 5y = 3
(man beachte das (x^(1/3))² = (x²)^(1/3) = x^(2/3))

Dann MNF ergibt: y1= 3, y2= -1/2

Rücksubs. ergibt dann: x1 = 27, x2= - 1/8

Allerdings klappt bei der Probe x2 dann nicht, daher nur 27 als Lösung.

 

[Schnitzel2k8]

Rücksubs. ergibt dann: x1 = 27, x2= - 1/8

Allerdings klappt bei der Probe x2 dann nicht, daher nur 27 als Lösung.

Dazu brauchst du keine Probe. Die Gleichung x^(1/3)=-1/2 hat keine Lösung!!!

 

[Pommbaer]

Dazu brauchst du keine Probe. Die Gleichung x^(1/3)=-1/2 hat keine Lösung!!!

Wieso ?
Wenn ich beide seiten hoch 3 nehme, dann komme ich auf x = -1/8
Nur bei den "geraden" Exponenten kann das Ergebnis nicht negativ sein ( komplexe Zahlen mal aussen vor )

Die Lösung gibt auch vor, dass 27 und -1/8 die Lösungen darstellen.

Die Ursprüngliche Gleichung war 2*(x²)^(1/3) - 5*(x)^(1/3) = 3

Danke für die Hinweise. das mit der Substitution habe ich mir in der Formelsammlung zum Thema Irrationale F'n notiert.

 

[Evilandi666]

Wenn man http://de.wikipedia.org/wiki/Wurzel_(Mathematik) durchliest,

ist zufällig genau (-2)³ = -8 die Ausnahme bei den negativen Wurzeln

Daher könnte man sowas schon mal prüfen...

Aber für die Schule ist sowas egal.

 

[Schnitzel2k8]

Dazu brauchst du keine Probe. Die Gleichung x^(1/3)=-1/2 hat keine Lösung!!!

Wieso ?
Wenn ich beide seiten hoch 3 nehme, dann komme ich auf x = -1/8
Nur bei den "geraden" Exponenten kann das Ergebnis nicht negativ sein ( komplexe Zahlen mal aussen vor )

Die Lösung gibt auch vor, dass 27 und -1/8 die Lösungen darstellen.

Die Ursprüngliche Gleichung war 2*(x²)^(1/3) - 5*(x)^(1/3) = 3

Danke für die Hinweise. das mit der Substitution habe ich mir in der Formelsammlung zum Thema Irrationale F'n notiert.

1. x^(1/3)=-1/2 heißt nicht, daß du einfach "hoch 3" nimmst und damit x hast. Die Aufgabe lautet: Finde ein x, dessen 3. Wurzel=-1/2 ist und so eines gibt es nicht!!

2. Falls du 1. nicht glaubst, setze mal -1/8 in die ursprüngliche Gleichung als Probe ein.

 

[Pommbaer]

Wenn ich in die Ursprungsgleichung -1/8 einsetze kommt das richtige Ergebnis raus.

Ebenso wenn ich in meinen Taschenrechner 3. Wurzel aus -1/8 eingebe.

x^(1/3)=-1/2 heißt nicht, daß du einfach "hoch 3" nimmst und damit x hast

Warum ? ich kann doch beide Seiten einfach "hoch 3" nehmen. Die Freiheit habe ich bei so einer Gleichung ja.
Dann steht auf der linken seite nurnoch X und rechts nurnoch -1/8

 

[Schnitzel2k8]

Wenn ich in die Ursprungsgleichung -1/8 einsetze kommt das richtige Ergebnis raus.

Ebenso wenn ich in meinen Taschenrechner 3. Wurzel aus -1/8 eingebe.

Schreib mal den Ausdruck selbst hin, dann siehst du es vielleicht. Dein Taschenrechner macht einen Fehler, siehe dazu auch den Wikipediaartikel: http://de.wikipedia.org/wiki/Wurzel_(Mathematik)#Zusammenhang_mit_Potenzen ->Wurzeln aus negativen Zahlen.

Der Artikel ist zwar auch sehr unsauber, aber ich bin zu faul jetzt ein entsprechendes Buch zu suchen. Der Artikel deutet es aber schon an. Wenn du diese Lösung zuläst, stößt du an anderer Stelle auf Probleme bzgl Konsistenz beim Rechnen mit Wurzeln.

Ich gebe dir noch ein Beispiel. Die komplexen Zahlen: Dort wird i^2=-1 definiert und nicht i=Wurzel(-1). Das hat einen Grund.

x^(1/3)=-1/2 heißt nicht, daß du einfach "hoch 3" nimmst und damit x hast

Warum ? ich kann doch beide Seiten einfach "hoch 3" nehmen. Die Freiheit habe ich bei so einer Gleichung ja.
Dann steht auf der linken seite nurnoch X und rechts nurnoch -1/8

Genau die Freiheit hast du eben nicht. Beim Lösen einer Gleichung darf man nur Äquivalenzumformungen vornehmen. In diesem Fall handelt es sich nicht um eine Äquivalenzumformung!!!

 

[Pommbaer]

Das würde aber in diesem Fall bedeuten, dass mein Matheprofessor ( der eher einer Maschine gleicht ) falsch liegt, da er -1/8x als Lösung angibt.
Dies ist wohlgemerkt eine Klausuraufgabe, bei der es keine volle Punktzahl gab/gibt wenn die Lösung unvollständig ist. Hätte es nach der Klausur Einwände gegeben, wäre die Lösung entsprechend abgeändert oder es zumindest vermerkt.
Das ist was mich in diesem Zusammenhang stutzig macht.

Hast du irgendwo eine Quelle die belegt, dass ich mit meiner Annahme falsch liege?

Mein zweiter Taschenrechner - ein Texas Instruments Ti-89 gibt die Lösung auch aus.

Bezüglich der ungeraden Wurzeln aus negativen Zahlen werden folgende Positionen vertreten:

* Wurzeln aus negativen Zahlen sind generell „verboten“. Beispielsweise ist \sqrt[3]{-8} also undefiniert. Die Lösung der Gleichung x3 = ? 8 wird geschrieben als x = -\sqrt[3]{8}.
* Wurzeln aus negativen Zahlen sind erlaubt, wenn der Wurzelexponent eine ungerade Zahl ist (3, 5, 7, …). Für ungerade Zahlen 2n + 1 gilt generell

\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}.

Ohne weitere Quelle sehe ich das so, dass du Position 1 vertrittst, während ich eher die Position 2 vertrete. jetzt wäre meine Frage: Wer legt es fest?