soweit ich mich erinnern kann, benötigt man für das Finden zweier Unbekannte auch 2 Gleichungen...
gegeben ist, afaiks, nur eine... nämlich:
10x^3 + 7 + 10^y = (x+17)^3
ausmultipliziert ist das:
10x^3 + 7 + 10^y = x^3 + 51x^2 + 867x + 4913
nach null umgestellt ist das:
9x^3 - 51x^2 - 867x - (4906 - 10^y) = 0
und da hört es mit meinen Kopf-Fähigkeiten auf...

mein Derive kann die Gleichung hingegen lösen...
heraus kommen folgende Gleichungen für X:
x1 = 34 * Sqrt( 10 ) * cos( acos( Sqrt( 10 ) * ( 539863 - 81 * 10^y ) / 982600 ) / 3 ) / 9 + 17 / 9
x2 = 17/9 - 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 + PI / 3 ) / 9
x3 = 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 ) / 9 + 17/9
und wenn man in die dritte Gleichung...
y = 4
einsetz, erhält man das Ergebnis, dass:
x3 = 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^4 - 539863 ) / 982600 ) / 3 ) / 9 + 17/9 = 6
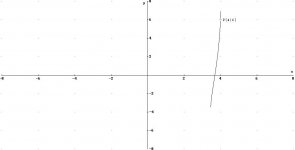
ich habe mir mal aus Juxx den Graphen der Funktion, die durch x3

repräsentiert wird, angeguckt...
sehr interessant (siehe Aufgabe.jpg)...
wie man sieht, ist die Gleichung nur für eine einzige natürliche Zahl erfüllt...
auf Basis dieser ist auch die nach 0 umgestellte Basisgleichung nur für eine natürliche Zahl erfüllt...
so ließe sich auf Basis der Analysis in Kombination mit einer korrekten Definition des Werte- und Definitionsbereichs das Ganze ohne Ausprobieren lösen...
mathematisch würde ich das in etwa so ausdrücken:
g = 34 * Sqrt( 10 ) * cos( acos( Sqrt( 10 ) * ( 539863 - 81 * 10^y ) / 982600 ) / 3 ) / 9 + 17 / 9
= 34 * Sqrt( 10 ) * cos( acos( Sqrt( 10 ) * ( 539863 - 81 * 10^y ) / 982600 ) / 3 ) / 9 + 17 / 9
h = 17/9 - 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 + PI / 3 ) / 9
= 17/9 - 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 + PI / 3 ) / 9
j = 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 ) / 9 + 17/9
= 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 ) / 9 + 17/9
// Y ist die Menge aller natürlichen Zahlen y,
// für die gilt, dass g eine natürliche Zahl ist,
eine natürliche Zahl ist,
// oder h eine natürliche Zahl ist,
eine natürliche Zahl ist,
// oder j eine natürliche Zahl ist
eine natürliche Zahl ist
Y = {y € N | g € N v h
€ N v h € N v j
€ N v j € N}
€ N}
f(x, y) = 9x^3 - 51x^2 - 867x - (4906 - 10^y)
// X ist die Menge aller natürlichen Zahlen x,
// die eingesetzt in f(x, y) = 0 ergeben,
// wobei y ein Element von Y soll soll
X = {x € N | f(x, y) = 0 ^ y € Y }
wie ich gerade bemerkt habe, kann man das ganze auch ein bissel kürzen, da g

, h

und j

ja bereits für eine Nullstelle ausgelegt sind und somit eine zusätzliche Prüfung gegen f(x, y) unnötig ist:
g = 34 * Sqrt( 10 ) * cos( acos( Sqrt( 10 ) * ( 539863 - 81 * 10^y ) / 982600 ) / 3 ) / 9 + 17 / 9
= 34 * Sqrt( 10 ) * cos( acos( Sqrt( 10 ) * ( 539863 - 81 * 10^y ) / 982600 ) / 3 ) / 9 + 17 / 9
h = 17/9 - 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 + PI / 3 ) / 9
= 17/9 - 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 + PI / 3 ) / 9
j = 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 ) / 9 + 17/9
= 34 * Sqrt( 10 ) * sin( asin( Sqrt( 10 ) * ( 81 * 10^y - 539863 ) / 982600 ) / 3 ) / 9 + 17/9
// X ist die Menge aller natürlichen Zahlen x,
// für die gilt, dass x = g ,
,
// oder x = h ,
,
// oder x = j ,
,
// wenn y eine natürliche Zahl ist
X = {x € N | ( x = g v x = h
v x = h v x = j
v x = j ) ^ y € N}
) ^ y € N}
ist allerdings schon ziemlich weit aus dem Fenster gelehnt - da wäre evtl. eine tiefere Analyse von g

und h

vorteilhaft...

oder um es ganz banal zu machen:
f(x, y) = 9x^3 - 51x^2 - 867x - (4906 - 10^y)
// X ist die Menge aller natürlichen X,
// für die die Gleichung f(x, y) = 0 erfüllt ist,
// wobei y eine natürliche Zahl ist
X = {x € N | f(x, y) = 0 ^ y € N}
wobei das nicht mehr wirklich etwas mit einer Lösung zu tun hat, eher mit einer schönen Formulierung der Aufgabenstellung...

aber rein von der Definition her sollte es klappen - man muss nur jemanden finden, der es wirklich ausrechnet...

cheers...
Edit1: X = {...} korrigiert
Edit2: Bild von f(x, 4) angehängt (Aufgabe_2.jpg)
Edit3: für den interessierten Leser die Extrema ausfindig gemacht (Aufgabe_3.jpg und Aufgabe_4.jpg)
Edit4: Textbeschreibung von X = {...} korrigiert
Edit5: Y = {...} korrigiert
Edit6: kürzere Definition hinzugefügt
Edit7: Bild mit g(x), h

und j

gemacht (Aufgabe_5.jpg)