Kleine Mathe Aufgabe, die ich nicht gelöst bekomme...

[MrTilman]

Hi,

ich würde gerne diese Mathematik-Aufgabe aus dem Buch meines Sohnes lösen, ich komme aber nicht auf die Lösung :facepalm: :huh:

Die Aufgabe ist folgende:

Auf der in Fig. 7 (siehe Skizze unten) abgebildeten dreieckigen Wiese soll ein Gebäude mit rechteckigem Grundriss so gebaut werden, dass es direkt an die Schlossallee und Parkstraße grenzt. Die verbleibenden beiden Dreiecke sollen als Grünflächen genutzt werden. Welche Maße würdest Du vorschlagen, sodass das Gebäude die Maximale Fläche ausnutzt.

Kurz eine Skizze mit Paint gezeichnet:



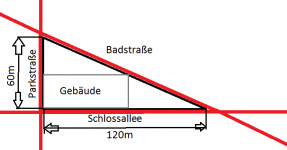
Beim den roten Linien handelt es sich um die Straßen.

Als Belohnung für den ersten, der die Aufgabe korrekt und vollständig gelöst hat (und bitte mit einer ausführlichen Erklärung) , gibt es die verbleibenden Teile aus meinem Verkaufsthread komplett kostenlos (nicht mal Versandkosten müsst Ihr zahlen!).

Viele Grüße
Tilman

 

[Lpz3sn]

sollte doch völlig egal sein... die grundfläche bleibt doch gleich... oder seh ich das falsch? ^^
edith: nur bei gleich langen schenkeln... hier also eher 30x60m ^^

 

[MrTilman]

Nein, leider nicht

EDIT: Doch, das letzte stimmt! Das Nein auf die erste Aussage bezogen!

 

[Thomebau]

das ist eigentlich eine relativ einfache Grenzwertaufgabe, aber nach der Abiprüfung scheine ich das gelöscht zu haben :facepalm:

 

[Ede_123]

Wenn du es "mathematisch" Lösen willst ist es ganz einfach:

Wähle Parkstraße = y-Achse und Schloßalee = x-Achse eines Kordinatensystems.
Dann ist jeder Punkt P(x,y) in der Fläche durch die Strecke nach rechts auf der Schloßalle x und die Strecke nach oben auf der Parkstraße festgelegt.

Dann kannst du die Badstraße als eine Funktion y(x) = -60m/120m * x + 60m beschreiben.

Dann ist die Grundfläche des Hauses einfach A(x) = x*y(x) und von dieser Funktion musst du nur noch das Maximum bestimmen.



Edit: Es geht auch ohne CAS iYassin ;-)

von oben: A(x) = x*y(x) = x* (-0.5*x + 60m) = -0.5 * x² + x*60m
Ableiten: A'(x) = 2*0.5*x + 60 m = -x + 60m

Bedingung für Extremum (Maximalwert oder Minimalwert): 0 = A'(x) = -x + 60m => x = 60
(die zweite Ableitung spare ich mir an der Stelle, sollte klar sein, dass es ein Maximum ist ;-) )

Damit muss die Ecke des Hauses auf dem Punkt P(x,y(x)) = P(60m,30m) liegen (also fast wie es in der Original Skizze eingezeichnet ist).

 

[Lpz3sn]

nur gut, dass ich maschinen aufstelle und ein landschaftsgestalter bin ^^

 

[iYassin]

Du musst die Funktion des Flächeninhaltes maximieren, das wäre in dem Fall f(x) = x * (- 0,5 x + 60). Gibt man das dann in ein CAS ein und lässt das Maximum im Intervall [0;120] berechnen, dann erhält man x = 60 als Maximum.

 

[fb1996]

Oder in den GTR , den sollte Dein Sohn haben

 

[ullrik]

x = 60 (und damit y = 30) wurde doch bereits vorgeschlagen. Und abgelehnt. Ich komm aber auch auf nix anderes, oder bin vom Mathelernen vollkommen verblödet

 

[oezix]

(60 - y)(120 - x) = (60 - y)(120 - (120 - 2y) = (60 - y)2y = 120y - 2y^2

das Ableiten ergibt 120 - 4y und auflösen nach y ergibt y=30 und x=60

wo hab ich nur ein Denkfehler gemacht, wenn (60,30) falsch sein sollen

 

[MrTilman]

Hmm, schwierig, wer hat es denn jetzt als erstes richtig gelöst? Lpz3sn oder Ede_123?

EDIT: 30*60 ist korrekt! War ein Missverständnis oben, das Nein war wie gesagt auf den Beitrag ohne EDIT bezogen.

 

[Miko]

Hallo Zusammen,

da muss man gar nichts rechnen. Da sich das Viereck in x sowie in y Richtung Linear verändert, aber die Fläche quadratisch abnimmt, ist es immer auf der halben Strecke Maximal.
Das gilt für alle Vierecke die in rechtwinklige Dreiecke gesetzt werden und an Ankathete und Gegenkathete anliegen.

Viele Grüße
Miko

 

[iYassin]

Edit: Es geht auch ohne CAS iYassin ;-)

von oben: A(x) = x*y(x) = x* (-0.5*x + 60m) = -0.5 * x² + x*60m
Ableiten: A'(x) = 2*0.5*x + 60 m = -x + 60m

Bedingung für Extremum (Maximalwert oder Minimalwert): 0 = A'(x) = -x + 60m => x = 60
(die zweite Ableitung spare ich mir an der Stelle, sollte klar sein, dass es ein Maximum ist ;-) )

Damit muss die Ecke des Hauses auf dem Punkt P(x,y(x)) = P(60m,30m) liegen.

Stimmt. Aber das habe ich seit dem Abi nicht einmal mehr gemacht...

 

[Lpz3sn]

30mx60m stimmt schon... nur könnte ich es nicht mathematisch begründen ^^

edith sagt; siehe Miko...

 

[fb1996]

Mein GTR sagt jedenfalls auch dass das Maximum von f(x) bei x=60 liegt, der Flächeninhaltt wäre damit 1800m²... Die Wertetabelle sagt dasselbe, bei x=60 der größte Wert, bei x<60 und >60 jeweils kleinere Werte...
Mathematisch begründbar:
f'(x) ist 0 und hat einen Vorzeichenwechsel von + nach -, was Bedingung für einen Hochpunkt des Graphen bzw. ein Maximum der Funktion ist...

Edit: VIEL zu langsam

 

[Ede_123]

Hmm, schwierig, wer hat es denn jetzt als erstes richtig gelöst? Lpz3sn oder Ede_123?

Wenn es um die Sachen aus dem Verkaufssthread geht: Für die habe ich ohnehin keine Verwendung, die kannst du gerne Lpz3sn oder z.B. der Spendenaktion zuführen.

Wenn es um Ruhm und Ehre geht: Ich natürlich!

 

[Lpz3sn]

ich kann das zeug auch nicht brauchen ^^... belastbar gelöst hat es ja eh ede ^^

ging ja schlag auf schlag hier ^^

 

[MrTilman]

Gut, mein Dank und der Rum und die Ehere gehen an Ede_123! Auch danke an alle anderen!

Die Sachen wandern dann eben zur Spendenaktion